Conway's Game of Life

Conway’s Game of Life is an example of cellular automata: a set of rules governing the behavior of a field made up of discrete cells. In practice, it creates a pretty animation to look at. You can draw out each step on graph paper, using the squares as cells. A filled-in square will be “alive” and an empty square will be “dead.” If a living square has two or three living neighbors, it continues to live on the next step. If a dead square has exactly three living neighbors, it comes alive on the next step. Every other square dies or remains dead on the next step. You can see an example of the progression of steps in the following figure.

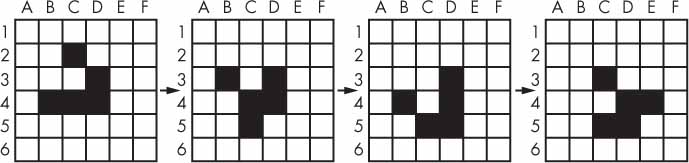
Even though the rules are simple, there are many surprising behaviors that emerge. Patterns in Conway’s Game of Life can move, self-replicate, or even mimic CPUs. But at the foundation of all of this complex, advanced behavior is a rather simple program.

We can use a list of lists to represent the two-dimensional field. The inner list represents each column of squares and stores a '#' hash string for living squares and a ' ' space string for dead squares. Type the following source code into the editor, and save the file as conway.py. It’s fine if you don’t quite understand how all of the code works; just enter it and follow along with comments and explanations provided here as close as you can:

# Conway's Game of Life
import random, time, copy
WIDTH = 60
HEIGHT = 20
FRAMES_PER_SECOND = 60

# Create a list of list for the cells:
nextCells = []
for x in range(WIDTH):
    column = [] # Create a new column.
    for y in range(HEIGHT):
        if random.randint(0, 1) == 0:
            column.append('#') # Add a living cell.
        else:
            column.append(' ') # Add a dead cell.
    nextCells.append(column) # nextCells is a list of column lists.

while True: # Main program loop.
    print('\n\n\n\n\n') # Separate each step with newlines.
    currentCells = copy.deepcopy(nextCells)

    # Print currentCells on the screen:
    for y in range(HEIGHT):
        for x in range(WIDTH):
            print(currentCells[x][y], end='') # Print the # or space.
        print() # Print a newline at the end of the row.

    # Calculate the next step's cells based on current step's cells:
    for x in range(WIDTH):
        for y in range(HEIGHT):
            # Get neighboring coordinates:
            # `% WIDTH` ensures leftCoord is always between 0 and WIDTH - 1
            leftCoord  = (x - 1) % WIDTH
            rightCoord = (x + 1) % WIDTH
            aboveCoord = (y - 1) % HEIGHT
            belowCoord = (y + 1) % HEIGHT

            # Count number of living neighbors:
            numNeighbors = 0
            if currentCells[leftCoord][aboveCoord] == '#':
                numNeighbors += 1 # Top-left neighbor is alive.
            if currentCells[x][aboveCoord] == '#':
                numNeighbors += 1 # Top neighbor is alive.
            if currentCells[rightCoord][aboveCoord] == '#':
                numNeighbors += 1 # Top-right neighbor is alive.
            if currentCells[leftCoord][y] == '#':
                numNeighbors += 1 # Left neighbor is alive.
            if currentCells[rightCoord][y] == '#':
                numNeighbors += 1 # Right neighbor is alive.
            if currentCells[leftCoord][belowCoord] == '#':
                numNeighbors += 1 # Bottom-left neighbor is alive.
            if currentCells[x][belowCoord] == '#':
                numNeighbors += 1 # Bottom neighbor is alive.
            if currentCells[rightCoord][belowCoord] == '#':
                numNeighbors += 1 # Bottom-right neighbor is alive.

            # Set cell based on Conway's Game of Life rules:
            if currentCells[x][y] == '#' and (numNeighbors == 2 or
numNeighbors == 3):
                # Living cells with 2 or 3 neighbors stay alive:
                nextCells[x][y] = '#'
            elif currentCells[x][y] == ' ' and numNeighbors == 3:
                # Dead cells with 3 neighbors become alive:
                nextCells[x][y] = '#'
            else:
                # Everything else dies or stays dead:
                nextCells[x][y] = ' '
    time.sleep(1/FRAMES_PER_SECOND) # Add a 1-second pause to reduce flickering.

Let’s look at this code line by line, starting at the top.

# Conway's Game of Life
import random, time, copy
WIDTH = 60
HEIGHT = 20
FRAMES_PER_SECOND = 60

First we import modules that contain functions we’ll need, namely the random.randint(), time.sleep(), and copy.deepcopy() functions.

# Create a list of list for the cells:
nextCells = []
for x in range(WIDTH):
    column = [] # Create a new column.
    for y in range(HEIGHT):
        if random.randint(0, 1) == 0:
            column.append('#') # Add a living cell.
        else:
            column.append(' ') # Add a dead cell.
    nextCells.append(column) # nextCells is a list of column lists.

The very first step of our cellular automata will be completely random. We need to create a list of lists data structure to store the '#' and ' ' strings that represent a living or dead cell, and their place in the list of lists reflects their position on the screen. The inner lists each represent a column of cells. The random.randint(0, 1) call gives an even 50/50 chance between the cell starting off alive or dead.

We put this list of lists in a variable called nextCells, because the first step in our main program loop will be to copy nextCells into currentCells. For our list of lists data structure, the x-coordinates start at 0 on the left and increase going right, while the y-coordinates start at 0 at the top and increase going down. So nextCells[0][0] will represent the cell at the top left of the screen, while nextCells[1][0] represents the cell to the right of that cell and nextCells[0][1] represents the cell beneath it.

while True: # Main program loop.
    print('\n\n\n\n\n') # Separate each step with newlines.
    currentCells = copy.deepcopy(nextCells)

Each iteration of our main program loop will be a single step of our cellular automata. On each step, we’ll copy nextCells to currentCells, print currentCells on the screen, and then use the cells in currentCells to calculate the cells in nextCells.

# Print currentCells on the screen:
    for y in range(HEIGHT):
        for x in range(WIDTH):
            print(currentCells[x][y], end='') # Print the # or space.
        print() # Print a newline at the end of the row.

These nested for loops ensure that we print a full row of cells to the screen, followed by a newline character at the end of the row. We repeat this for each row in nextCells.

    # Calculate the next step's cells based on current step's cells:
    for x in range(WIDTH):
        for y in range(HEIGHT):
            # Get neighboring coordinates:
            # `% WIDTH` ensures leftCoord is always between 0 and WIDTH - 1
            leftCoord  = (x - 1) % WIDTH
            rightCoord = (x + 1) % WIDTH
            aboveCoord = (y - 1) % HEIGHT
            belowCoord = (y + 1) % HEIGHT

Next, we need to use two nested for loops to calculate each cell for the next step. The living or dead state of the cell depends on the neighbors, so let’s first calculate the index of the cells to the left, right, above, and below the current x- and y-coordinates.

The % mod operator performs a “wraparound.” The left neighbor of a cell in the leftmost column 0 would be 0 - 1 or -1. To wrap this around to the rightmost column’s index, 59, we calculate (0 - 1) % WIDTH. Since WIDTH is 60, this expression evaluates to 59. This mod-wraparound technique works for the right, above, and below neighbors as well.

# Count number of living neighbors:
numNeighbors = 0
if currentCells[leftCoord][aboveCoord] == '#':
    numNeighbors += 1 # Top-left neighbor is alive.
if currentCells[x][aboveCoord] == '#':
    numNeighbors += 1 # Top neighbor is alive.
if currentCells[rightCoord][aboveCoord] == '#':
    numNeighbors += 1 # Top-right neighbor is alive.
if currentCells[leftCoord][y] == '#':
    numNeighbors += 1 # Left neighbor is alive.
if currentCells[rightCoord][y] == '#':
    numNeighbors += 1 # Right neighbor is alive.
if currentCells[leftCoord][belowCoord] == '#':
    numNeighbors += 1 # Bottom-left neighbor is alive.
if currentCells[x][belowCoord] == '#':
    numNeighbors += 1 # Bottom neighbor is alive.
if currentCells[rightCoord][belowCoord] == '#':
    numNeighbors += 1 # Bottom-right neighbor is alive.

To decide if the cell at nextCells[x][y] should be living or dead, we need to count the number of living neighbors currentCells[x][y] has. This series of if statements checks each of the eight neighbors of this cell, and adds 1 to numNeighbors for each living one.

# Set cell based on Conway's Game of Life rules:
            if currentCells[x][y] == '#' and (numNeighbors == 2 or
numNeighbors == 3):
                # Living cells with 2 or 3 neighbors stay alive:
                nextCells[x][y] = '#'
            elif currentCells[x][y] == ' ' and numNeighbors == 3:
                # Dead cells with 3 neighbors become alive:
                nextCells[x][y] = '#'
            else:
                # Everything else dies or stays dead:
                nextCells[x][y] = ' '
    time.sleep(1/FRAMES_PER_SECOND) 

Now that we know the number of living neighbors for the cell at currentCells[x][y], we can set nextCells[x][y] to either '#' or ' '. After we loop over every possible x- and y-coordinate, the program takes a 1/60-second pause by calling time.sleep(1/FRAMES_PER_SECOND). Then the program execution goes back to the start of the main program loop to continue with the next step.

Several patterns have been discovered with names such as “glider,” “propeller,” or “heavyweight spaceship.” The glider pattern results in a pattern that “moves” diagonally every four steps. You can create a single glider by replacing this line in our conway.py program:

if random.randint(0, 1) == 0:

with this line:

if (x, y) in ((1, 0), (2, 1), (0, 2), (1, 2), (2, 2)):

You can find out more about the intriguing devices made using Conway’s Game of Life by searching the web. And you can find other short, text-based Python programs like this one at https://github.com/asweigart/pythonstdiogames.